MOTO INTORNO AD UN PROFILO ALARE

Prima di analizzare il campo di velocità e di pressione associato ad un moto uniforme che investe un profilo alare facciamo ancora qualche considerazione sul valore della circolazione.

Apparentemente la circolazione intorno al profilo (e dunque al cilindro) può essere assegnata ad arbitrio. Il moto attorno al cilindro dà luogo, sul profilo, a due punti di ristagno, che si spostanto lungo il profilo al variare della circolazione. Esiste un particolare valore della circolazione che porta il punto di ristagno di valle in corrispondenza della cuspide.

Questa condizione, che individua attraverso semplici considerazioni geometriche quale deve essere il valore della circolazione, è la condizione di Kutta.

Utilizzando la condizione di Kutta la circolazione non è più una variabile libera ed è possibile determinare la portanza di un profilo alare fissando la sua geometria e conoscendo il moto ad infinito. Si noti che i campi di moto ottenuti per un valore qualsiasi della circolazione sono tutti soluzioni valide del moto irrotazionale intorno al profilo. La condizione di Kutta fissa un particolare valore della circolazione per il quale il campo di velocità e di pressione bene approssima il reale moto intorno al profilo.

Cerchiamo di fornire un'interpretazione fisica della condizione di Kutta: per fare ciò è necessario utilizzare alcuni concetti che esulano dalla teoria dei moti irrotazionali ideali e che riguardano gli effetti associati alla viscosità di un fluido reale.

Supponiamo di partire da una situazione di quiete e di mettere in moto il profilo con una velocità piccola. La quiete è un caso particolare di moto irrotazionale, per cui, trascurando gli effetti viscosi, il moto, per il teorema di Thompson deve mantenersi irrotazionale.

Il campo di moto sarà dunque quello associato ad una circolazione nulla, in cui i due punti di ristagno si trasformano in due punti, l'uno sulla faccia inferiore in prossimità del bordo di attacco del profilo, e l'altro sulla faccia superiore in prossimità del bordo di uscita.

In un intorno della cuspide si realizza una situazione molto poco plausibile: una particella fluida prossima alla faccia inferiore del profilo dovrebbe viaggiare lungo il profilo stesso, fare una brusca inversione in corrispondenza della cuspide, muoversi controcorrente sulla faccia superiore del profilo fino a raggiungere il punto di ristagno e finalmente lasciare profilo. Un fluido reale non può comportarsi in questo modo. La viscosità del fluido tenderà ad attenuare il forte gradiente di velocità lungo il profilo, lo strato limite separerà e si formerà una scia con emissione di un vortice orario in corrispondenza della cuspide.

Poichè la circolazione lungo una curva che comprenda profilo e vortice deve mantenersi nulla, a questo fenomeno corrisponde la comparsa di una circolazione antioraria intorno al profilo. Ma una circolazione intorno al profilo fa sì che i punti di ristagno, come visto, si spostino e in particolare il punto di ristagno di valle si sposterà verso la cuspide. Il processo emissione di vorticità -> aumento della circolazione intorno al profilo -> spostamento del punto di ristagno verso la cuspide procede fino a che il punto di ristagno non finisce per raggiungere la cuspide stessa, annullando così la singolarità e creando una situazione in cui la viscosità non ha più necessità di provvedere all'eliminazione dei forti gradienti di velocità e l'emissione di vorticità cessa. Si realizza dunque una configurazione di ``equilibrio'' in cui la circolazione intorno al profilo non cambia più.

Alla luce di queste considerazioni esaminiamo ora i campi di velocità e pressione che si realizzano intorno ad un profilo alare investito da una corrente uniforme con l'aiuto di alcune animazioni che mostrano cosa accade quando varia l'angolo di attacco (efficace). In ogni fotogramma il campo di moto è ottenuto imponendo la condizione di Kutta per determinare la circolazione.

Si consiglia di consultare le pagine seguenti in sequenza, almeno la prima volta.

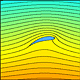
Funzione di corrente	Linee di fumo	Campo di velocità	Campo di pressione	Azioni sul corpo