MOTI IRROTAZIONALI PIANI DI FLUIDI IDEALI

Perché un aereo vola? La risposta è semplice: perché la forza esercitata dall'aria sulle ali dell'aereo è uguale al peso dell'aereo stesso. Un pò meno semplice è capire perché l'aria esercita una forza sulle ali di un aereo in moto e soprattutto conoscere l'intensità di questa forza in funzione delle caratteristiche geometriche dell'ala stessa.

Questa lezione è dedicata allo studio dei moti irrotazionali piani di fluidi ideali, ed ha come scopo ultimo proprio la determinazione della forza esercitata da una corrente in moto uniforme su di un profilo alare, la cosiddetta portanza. Tale formulazione può essere pensata come quella che si realizza intorno ad un profilo alare in moto con velocità costante in un fluido fermo, e quindi consente di rispondere, almeno qualitativamente, al precedente quesito.

Ricordando che per un fluido ideale le forze esercitate sul contorno - in questo caso il profilo - sono solo normali e dovute alla pressione, la soluzione procede attraverso la determinazione del campo di velocità e del campo di pressione per giungere alla distribuzione della pressione lungo il profilo e quindi alla determinazione della forza risultante.

Si dimostra come la forza risultante abbia un'unica componente perpendicolare alla direzione del moto (portanza) che è proporzionale alla circolazione intorno al profilo. La componente della risultante nella direzione del moto (resistenza) è sempre nulla. Tale apparente paradosso può essere risolto solo rimuovendo l'ipotesi di irrotazionalità e di idealità del fluido in prossimità del profilo, dove gli effetti viscosi, confinati all'interno del cosiddetto strato limite, sono comunque significativi e il moto è viscoso e rotazionale.

Lo studio dello strato limite, che esula dalla presente lezione, fornisce comunque l'importante informazione che, in assenza di fenomeni di separazione, le azioni di pressione vengono trasmesse inalterate attraverso lo strato limite, per cui le informazioni sulla portanza ottenute nel seguito forniscono una buona approssimazione del valore reale della portanza di un profilo.

La lezione si svilupperà secondo il seguente schema:

	Richiami sulla teoria dei moti irrotazionali piani Si riprendono alcune nozioni elementari di Meccanica dei Fluidi funzionali alla comprensione del metodo di soluzione.
	Esempi di moti irrotazionali piani elementari Vengono illustrati alcuni moti irrotazionali piani la cui soluzione è ottenibile per via analitica e la cui composizione consente di realizzare moti piu' complessi.
	Moto intorno ad un cilindro Viene analizzato il moto intorno ad un cilindro in termini di campo di velocità e di pressione. Alcune animazioni mostrano come la soluzione vari al variare della circolazione intorno al cilindro.
	La trasformazione di Joukowski Viene introdotta la trasformazione conforme di Joukowski che consente di trasformare il dominio esterno ad un cilindro nel dominio esterno ad un profilo alare. Un'applicazione interattiva consente di vedere come la forma del profilo vari al variare dei parametri della trasformazione.
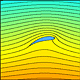	Moto intorno ad un profilo alare Viene analizzato il moto intorno ad un profilo alare in termini di campo di velocità e di pressione. Alcune animazioni mostrano come la soluzione varia al variare dell'angolo di attacco.

Si consiglia di consultare le varie pagine in sequenza, almeno la prima volta.

Torna alla copertina