Bevor wir das Geschwindigkeits- und Druckfeld für ein Tragflächenprofil analysieren, müssen wir etwas gründlicher die Rolle der Zirkulation untersuchen.

Das Kutta-Joukowski-Theorem zeigt, daß der Auftrieb proportional zur Zirkulation ist, aber offensichtlich kann der Betrag der Zirkulation willkürlich zugeordnet werden.

Die Lösung für die Strömung um einen Zylinder legt nahe, daß wir am Tragflächenprofil theoretisch zwei Staupunkte finden können, deren Positionen von der Zirkulation um das Profil abhängen. Es gibt einen bestimmten Wert der Zirkulation, bei dem der rückwärtige Staupunkt (V=0) sich genau auf die Hinterkante zu bewegt.

Diese Bedingung, die einen Wert der Zirkulation durch rein geometrische Betrachtungen festsetzt, ist die Kutta-Bedingung.

Unter Verwendung der Kutta-Bedingung ist die Zirkulation keine freie Variable mehr und es ist möglich, den Auftrieb des Profils mit denselben Methoden wie für den Zylinder zu berechnen. Man beachte, daß alle Strömungsfelder, die man für einen festen Wert der Zirkulation erhält, gültige Lösungen der Strömung um ein Tragflächenprofil sind. Die Kutta-Bedingung beschreibt eines dieser Felder, und zwar jenes, welches am besten die reale Strömung wiedergibt.

Wir können versuchen, eine praktikable physikalische Erklärung für die Kutta-Bedingung zu geben; um dies zu tun, müssen wir einen Begriff einführen, der von der Theorie der wirbelfreien, nichtviskosen Strömung außer Acht gelassen wird: Die Rolle der Viskosität eines realen Fluids.

Angenommen, wir gehen von einer statischen Situation aus und geben dem Fluid eine kleine Geschwindigkeit. Wenn das Feld anfänglich in Ruhe ist, ist es auch wirbelfrei, und bleibt - bei Vernachlässigung der Viskosität - wirbelfrei aufgrund des Thompsonschen Theorems.

Das Strömungsfeld um den Flügel hat dann keine Zirkulation, wobei der eine Staupunkt auf der Unterseite des Flügels nahe der Vorderkante und der andere Staupunkt auf der Oberseite nahe der scharfen  Hinterkante liegt.

Eine sehr unwahrscheinliche Situation wird an der Hinterkante geschaffen: Ein Teilchen des Fluids an der Unterseite der Tragfläche müßte sich entlang des Profils bewegen, eine scharfe Kurve an der Hinterkante machen, an der Oberseite stromaufwärts fließen, bis es den Staupunkt erreicht, und dann schließlich den Rand des Profils verläßt. Ein reales Fluid kann sich nicht so verhalten. Viskosität bewirkt eine Dämpfung des scharfen Geschwindigkeits-Gradienten entlang des Profils, Ablösung der Grenzschicht findet statt und es bildet sich ein Sog mit einer von der Hinterkante ausgehenden Verwirbelung im Uhrzeigersinn (bei einer Ausrichtung des Profils mit der Vorderkante nach rechts und einer von rechts kommenden Anströmung).

Da die Zirkulation entlang einer Kurve, die den Wirbel und das Profil einschließt, immer noch Null sein muß, führt dies zu einer Zirkulation gegen den Uhrzeigersinn um das Profil. Wenn jedoch eine von Null verschiedene Zirkulation um den Flügel existiert, bewegen sich die Staupunkte; speziell der hintere Staupunkt bewegt sich auf die Hinterkante zu. Die Sequenz Ablösen eines Wirbels ->
Ansteigen der Zirkulation um das Tragflächenprofil -> stromabwärtiges Abwandern des hinteren Staupunktes dauert an, bis der Staupunkt die scharfe Hinterkante erreicht. Wenn dies passiert, verschwindet der scharfe Geschwindigkeits-gradient und das Ablösen von Wirbeln hört auf. Diese "Gleichgewichts"-Situation bestimmt  den Wert der Zirkulation um das Profil, welcher sich dann nicht mehr ändert.

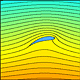
Nun wollen wir die Geschwindigkeits- und Druckfelder um ein Tragflächenprofil mit Hilfe einiger Animationen untersuchen, die zeigen, wie diese Felder bei Änderung des (effektiven) Anstellwinkels variieren. In jedem Einzelbild erhält man das Strömungsfeld, indem man unter Verwendung der Kutta-Bedingung die Zirkulation bestimmt.

Es wird empfohlen, die verschiedenen Seiten in Reihenfolge anzuschauen, vor allem für neue Besucher.
 

Strom- funktion	Rauch- linien	Geschwindig- keitsfeld	Druck- feld	Kräfte auf den Körper