

Wir führen die konforme Transformation nach Joukowski ein:
![]()
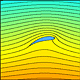
und untersuchen, wie ein in der z-Ebene definierter Zylinder mit Radius R in die zí-Ebene abgebildet wird:
In der folgenden interaktiven Anwendung kann man den
Mittelpunkt des Kreises in der z-Ebene mit Hilfe der Schaltflächen
hin- und herbewegen und das sich dadurch ergebende
Tragflächenprofil sehen.
 |
 |
| JDK-1.0 | JDK-1.1 |
Hier ist es zweckmäßig, einige Begriffe über Joukowski-Tragflächenprofile einzuführen.

Joukowski-Tragflächenprofile haben eine runde
Vorderkante und eine spitz zulaufende bzw. scharfe Hinterkante, wo die
Skelettlinie einen Winkel 2![]() mit der
Profilsehne einschließt. In der transformierten Zylinderebene
wird
mit der
Profilsehne einschließt. In der transformierten Zylinderebene
wird ![]() eingeschlossen vom Radius, der die negative
x-Achse berührt, und der Horizontalen, so daß
eingeschlossen vom Radius, der die negative
x-Achse berührt, und der Horizontalen, so daß
![]()
Normalerweise ist der Anstellwinkel (auch als
physikalischer Anstellwinkel bezeichnet) definiert als der
Winkel ![]() , den die gleichförmige
Strömung mit der Horizontalen einschließt. Von
größerem Interesse für die Aerodynamik ist der
Winkel
, den die gleichförmige
Strömung mit der Horizontalen einschließt. Von
größerem Interesse für die Aerodynamik ist der
Winkel
![]()
Wenn der Winkel ![]() Null ist,
verschwindet der Auftrieb. Somit wird der Winkel
Null ist,
verschwindet der Auftrieb. Somit wird der Winkel ![]() oft auch als effektiver Anstellwinkel
definiert.
oft auch als effektiver Anstellwinkel
definiert.
INDEX
 |
 |
 |
 |
 |
 |