Copyright © 1999 jsd
David Anderson and Scott Eberhardt recently wrote a paper called "How Airplanes Fly: A Physical Description of Lift". Versions were published in various places including the EAA journal Sport Aviation and Discover magazine. There is also a book-length version published by McGraw-Hill. The online version at http://www.aa.washington.edu/faculty/eberhardt/lift.htm seems to have been taken down, but you can still find it via the Wayback Machine at archive.org. The content at http://www.allstar.fiu.edu/aero/airflylvl3.htm appears to be very similar. A ``revised'' version can be found at http://www.allstar.fiu.edu/aero/Flightrevisited.pdf
The paper makes several valid points. These include
1) The notion that the air passing above and below the wing must do so in equal time is totally false.
2) The notion that a wing must be curved on top and flat on the bottom is totally false.
3) Given the velocity field near a wing, we can calculate the
lift by considering how the air is deflected and using the principle
of conservation of momentum.
The paper contains a number of significant errors. These include:
1) The paper contains the statements «This upwash actually contributes to negative lift and more air must be diverted down to compensate for it.» and «upwash is accelerating air in the wrong direction for lift.»
It is easy to see that these statements are wrong. Suppose you are standing on a plank overhanging a trampoline. You throw a baseball downward, rather hard. During the throwing motion, the recoil forces you upward a little. Now suppose the baseball bounces off the trampoline, comes back up, and is caught by you. Interestingly, when you catch the ball you are forced upward again. The analogy to airplanes is clear: both the incoming upwash and the outgoing downwash make positive contributions to the lift.
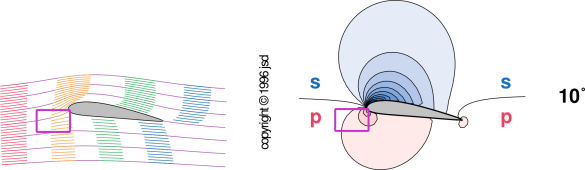
People who have only a superficial understanding of upwash sometimes assume that the wing is sucking the air up. They suppose that there is a low pressure region just below the front of the wing, pulling up on the air and (by the same token) pulling down on the wing.
There is only one problem with this suck-up theory. The problem is that it is wrong. If you look at the actual flow patterns and pressure patterns, you will see that the air in the upwash region is flowing up a pressure gradient. It is carried by its own momentum into regions of higher and higher pressure, as shown in the following figure.

For details on what the curves in this figure mean, see http://www.av8n.com/how/htm/airfoils.html.
This flow into a high pressure region is not a matter of opinion. It is a carefully calculated consequence of the equations of motion.
2) In addition to the just-mentioned misunderstanding of the
contribution
that upwash makes to the force and momentum budget, the paper
misunderstands the contribution that upwash makes to the energy
budget. Let us consider the baseball analogy again. Suppose you
throw the baseball at such an angle that it bounces between the
itrampoline and the plank several times, as suggested by the following
figure:
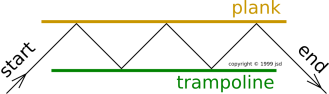
To be sure, when you first throw the baseball, you must expend energy. On the other hand, each bounce off the bottom of the plank transfers upward momentum to you, without further expenditure of energy. This analogy proves the paper is quite wrong to assume that the size of the momentum transfer tells you the size of the energy transfer.
The analogy to airplanes is this: Obviously, the airplane must expend some energy to create the circulatory motion that is responsible for the upwash and downwash. However, after the circulation is established, it tends to perpetuate itself with only rather minor additional energy inputs. The energy of the downwashing air bounces off the lower air and returns in the upwash. (You should not imagine that any typical air molecule makes a round trip. The energy nevertheless returns, after being passed from molecule to molecule.) The contributions are summarized in the following table
| energy contribution | momentum contribution | |
| upwash | input | upward |
| downwash | output | upward |
The fact that in my analogy, the plank and the trampoline were relatively close does not mean that upwash only contributes when the airplane is near the ground. The air near the wing is perfectly capable of "bouncing" off the lower air, no matter how high the airplane is flying. You would never learn this by armchair experiments such as pushing the air around with your hand, because your hand is too small, too slow, and not airfoil-shaped.
This is worth knowing because it explains why gliders have long, skinny wings. A glider with a sufficiently large aspect ratio could in principle produce lift with arbitrarily little induced drag, because the positive and negative energy contributions of the upwash and downwash would just cancel. For an ordinary finite-span wing, the upwash energy mostly but never entirely compensates for the energy carried off in the downwash.
Since the paper does not correctly account for the energy of the upwash, its calculation of induced drag is wrong. It is not merely wrong in principle, it is wrong in ways that lead you astray, as will be discussed below.
3) The paper has a whole section called «the
wing as a pump», suggesting that a wing is analogous
to a pump. This is a bad analogy. Bernoulli's principle does not
apply to the air in pumps, but it does apply (to a very useful
approximation) to the air near a wing.
4) The paper also draws an analogy between a wing and a scoop. This is also a bad analogy. The paper says that the «the height [of the scoop] is somewhat related to the chord length». This makes a nice intuitive picture, but it just isn't how wings work. In particular, consider what happens if we start with an ordinary airplane, where the wing has an aspect ratio of about 8, and replace the wing with one that has an aspect ratio of about 20, such as might be found on a glider. We do this by making the chord smaller and the span larger, keeping the wing area constant.
| The scoop theory predicts that the glider wing grabs only a small amount of air (because of its small chord). | A correct analysis indicates that the glider wing actually affects the air for a larger distance above and below the wing. Its influence extends for a distance that depends on the span, not the chord. |
| The scoop theory predicts that the glider wing has about 15% less induced drag than the short, fat wing. | A correct analysis indicates that the glider wing actually has about 615% (i.e. more than a factor of 6) less induced drag than the short, fat wing. |
5) The scoop model predicts that ground effect should gradually become noticeable starting when the wing is within a chord-length of the ground. This is wrong. In fact, we know from standard engineering equations and common pilot experience that ground effect gradually becomes significant starting when the wing is within a span length of the ground.
We know that flying in ground effect makes the wing more efficient. The paper tries to explain this by claiming «the upwash is reduced because the ground inhibits the circulation». This is quite wrong. As mentioned above, to produce the required lift with more efficiency you need more upwash.
The ground does not significantly inhibit the circulation (i.e. the line integral of velocity) around the wing. There are several ways to prove that if you managed to get rid of the circulation you would also get rid of the lift. You could prove it using the Kutta-Zhukovsky theorem, or you could get the same answer by using Bernoulli's principle: no circulation => no difference in velocity => no difference in pressure => no lift.
6) The paper cites the Coanda effect as a plausibility argument in favor of the scoop theory. Alas, for reasons spelled out at
http://www.av8n.com/how/htm/spins.html#sec_coanda
using the Coanda effect to explain the operation of a normal wing makes about as much sense as using bowling to explain walking. To be sure, bowling and walking use some of the same muscle groups, and both fundamentally rely on Newton's laws, but if you don't already know how to walk you won't learn much by considering the additional complexity of the bowling situation.
Furthermore, if you actually carry out the experiment suggested in the paper, it gives evidence against the claim that the airfoil affects the fluid for a distance «somewhat related to the chord length». If you touch a chopstick or some other small object against a large stream of water, you will find that the thickness of water that follows the curve is much less than a chord length. In contrast, a real wing affects the air over a distance much larger than the chord. The Coanda effect is just not a good model for how wings work.
7) In the paper and elsewhere, the authors have calculated estimates of the size of the scoop and the amount of air deflected. These calculations require assuming standard lift formulas that do not come from the scoop theory itself, but come from some other theory. Any attempt to use such calculations as evidence in favor of the scoop theory would be an invalid circular argument. To say it another way, the scoop theory could never be considered a complete theory; you would have to explain the other theory before you could begin to use the scoop theory.
8) Although in one place the paper correctly says that «there is nothing wrong with the Bernoulli principle», in numerous other places it leaves the impression that Professor Bernoulli is somehow to blame for the "equal transit time" fallacy and/or the "curved on the top / flat on the bottom" fallacy. Any tool can be used properly or improperly. Millions of students have invoked Newton's laws improperly, but we don't let that stop us from applying them properly when we get the chance. By the same token we should not teach people to disrespect Bernoulli's principle.
9) The paper implies that friction plays a central role in making
the air follow the curve of the wing. For example, it says «Why
should a fluid follow a curved surface? The answer is viscosity»
This is nonsense. The truth is almost diametrically opposite:
a wing works better when the fluid has less viscosity (as
long as the viscosity is not exactly zero).
The paper says «We hope that the answers
provided here will clarify many misconceptions about lift and
that you will adopt our explanation when explaining lift to others.»
I agree that the paper makes two or three valid points about common
misconceptions. Alas, it goes on to replace those common misconceptions
with a string of other misconceptions.
I urge you not to use the scoop theory when explaining
lift to others.
By way of constructive counter-offer, a pilot-oriented explanation of how wings really work can be found at
http://www.av8n.com/how/htm/airfoils.html
Comments can be sent to jsd@av8n.com